私は以前から、人工知能や機械学習を学んでみたいと強く思っていた。しかし実際に数冊本を購入して勉強を試みたところ、残念ながら途中で挫折してしまった。
Webプログラミングに関しては、プログラミングスクール「ウェブカツ!!」の動画教材が私の性分に合っていたのか、すんなりと身に付けることができた。
人工知能や機械学習も、動画教材であれば同様にうまく学習できるのではないかという淡い期待を抱きつつ、Udemyで講座を探したところ、以下の講座がとても評判が良いようだ。
>> 【キカガク流】人工知能・機械学習 脱ブラックボックス講座 – 初級編 –
実際に購入し視聴してみたが、評判通りの非常に分かりやすい講義だった。機械学習を学ぶ上で必要となる数学も丁寧に説明されている。動画学習の利点は、効率が良く知識のイメージが得られる点にあると思う。知識の整理や詳細の学習に書籍は欠かせないが、何かを学ぶ上でまずは動画で全体のイメージを得るというのは、とても効率が良い学習方法であると思う。
この記事は、上記「【キカガク流】~ – 初級編 – 」で学んだことを自分の中で整理するためにまとめているだけなので、詳細を知りたい方はUdemyの動画を視聴してほしい。
人工知能・機械学習・ディープラーニングの違い
人工知能(AI)、機械学習、ディープラーニングの技術的な位置付けは、図で表すと次のようになる。
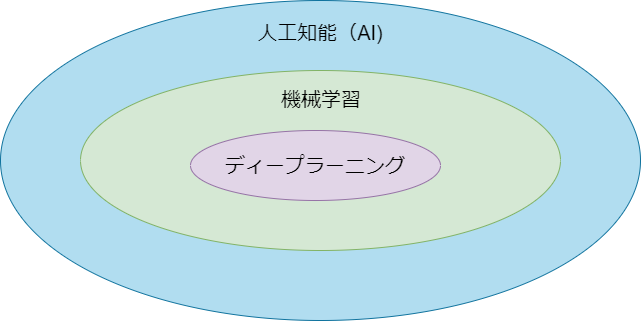
つまり、ディープラーニングと呼ばれる技術は、機械学習という技術の一部であり、また、機械学習は人工知能(AI)に関する技術の一部であるということ。
人間と同等の仕事をコンピュータに行わせる技術が人工知能(AI)だ。ただし、人間が持つ機能をコンピュータに落とし込むためには、次のようないくつかの処理について考える必要がある。
- 人間であれば目から光の情報を、耳で音の情報を取得しているが、コンピュータでこれを行うためには、センサーで情報を取得する必要がある。
- 目からの情報であれば画像データに、耳からの情報であれば音声データにそれぞれ変換して、コンピュータ内部で扱える形にする必要がある。
- 目からの情報(画像データ)や耳からの情報(音声データ)など、複数の異なる形式の情報を統一した形式に変換し、コンピュータが計算できる数値として表現する必要がある。
- コンピュータが扱える数値に変換された情報(入力X)から、何らかの判断(出力Y)を下すためのロジックが必要になる。
- コンピュータ自ら、入力X(例えば画像)から出力Y(猫の画像であるかどうか)を判定するためのロジックを見つけ出させるためには、大量のデータからコンピュータに学習させる必要がある。
これらのことを図に表すと次のようになる。
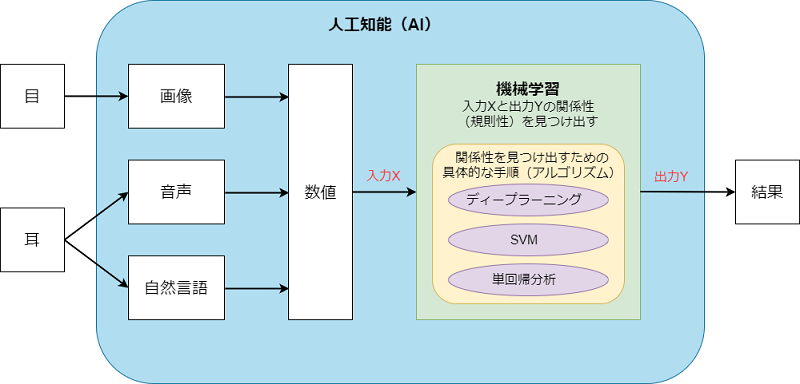
このように機械学習は、コンピュータ内部で数値化された入力Xから出力Yを得るための規則(ロジック)を見つけ出すための技術だ。
一方、ディープラーニングは、そのような規則を見つけ出すためのアルゴリズム(手順)の1つに過ぎない。他にもSVM(サポート・ベクター・マシーン)や単回帰分析など多数のアルゴリズムが存在する。
また、ディープラーニングは学習データの数が多くないとうまく機能しない、単回帰分析はデータの数がそれほど多くなくても機能するが小回りが利かない、などの特徴がある。
このように各アルゴリズムにはそれぞれメリット・デメリットが存在するため、常にディープラーニングを用いるのが最適というわけではない。
この講座 「【キカガク流】~ – 初級編 – 」 では、単回帰分析に焦点を当てて、機械学習の初歩を分かりやすく説明してくれている。理解するための数学の知識や、プログラムを組むための Python の講義もふくまれているので、人工知能・機械学習の勉強を始めたいと思っている人にオススメな講座だ。
>> 【キカガク流】人工知能・機械学習 脱ブラックボックス講座 – 初級編 –
機械学習に必要な数学
機械学習で必要になる数学は、主に次の3つ。
- 微分・積分
- 線形代数
- 確率・統計
これらの知識がないと、機械学習を理解することはできない。ただ、それぞれの分野について網羅的な知識が必要かというと、そうではなく、機械学習を学ぶという観点からは必要のない事柄も多い。
この講座 「【キカガク流】~ – 初級編 – 」 では、機械学習を学ぶという観点から必要となる数学の知識を最小限に絞り、機械学習を学びながら必要な数学も学んでいくというスタイルをとっている。
機械学習の3大トピック
上で、「機械学習は、入力Xと出力Yの関係性を見つけるための技術」と説明したが、実はそれは機械学習のもつ1トピック(教師あり学習)に過ぎず、機械学習には大きく分けると次の3つのトピックが存在する。
- 教師あり学習
- 教師なし学習
- 強化学習
教師あり学習
「教師あり学習」とは機械学習の手法の一つであり、これが先ほどの「入力Xと出力Yの関係性を見つけるための技術」に該当する。
そしてこの教師あり学習は、さらに次の2つのトピックに分けられる。
- 回帰 ーー 数値(連続値)を予測するための手法
例:部屋の広さXから家賃Yを予測する。 - 分類 ーー カテゴリを予測するための手法
例:ワインのアルコール度数Xから種類Y(赤ワイン or 白ワイン)を予測する。
教師あり学習は、「何か(出力Y)を予測したい」という課題に対して用いられる手法といえる。
教師なし学習
教師あり学習が「何か(出力Y)を予測したい」という課題に対して使用される方法なのに対し、教師なし学習は、「データ(入力X)の特性を知りたい」という課題に対して使用される方法。学習の際に、正解となる出力Yが与えられない、という特徴がある。
教師なし学習は、大きく分けると次の2つのトピックがある。
- クラスタリング ーー ある集団(入力X)から似ている特徴を見出し、分類するための手法
- 次元削減
強化学習
強化学習は、学習させるためのデータX、Yを与えずに、試行錯誤を通じて一番いい行動を学習させる手法。
教師あり学習
内挿と外挿
- X = 1, Y = 2
- X = 2, Y = 4
- X = 4, Y = 8
という学習データ(過去のデータ)があったとする。このデータから「X = 3」のときのYの値を予測することはOKだが、「X = 5」のときのYの値を予測することはダメ。
「X = 3」のような学習データの範囲内(X = 1 ~ 4)の領域で予測することを内挿という。一方で、「X = 5」のような学習データの範囲外の領域で予測することを外挿という。
教師あり機械学習では、内挿の領域内でしか予測できることを保証しない。外挿の領域での予測は保証外なので注意が必要。
株価の予測は可能か?
過去のデータから未来の株価を予測することを考えた場合、時間という視点で考えると、未来の価格を予測することは外挿なのだから、未来の株価の予測に教師あり学習を使用できないのか?
時系列のデータの場合は、学習データの株価の範囲内なら内挿になるらしい。一方で、学習データの範囲外の株価は外挿となり予測することはできない。
微分
機械学習を学ぶ上で必須の数学の一つである微分。
微分の「数学としての意味」と「実用的にどの様に使用するのか」ということを知っておくことで、機械学習における微分の理解が捗るようになる。
微分の数学としての意味
微分とは数学において、グラフの接線の傾きを求める方法を意味する。例えば、次のようなグラフの関数 y=f(x) に微分という方法を適用することで、x = 1 などにおけるグラフの接線の傾きを求めることができる。
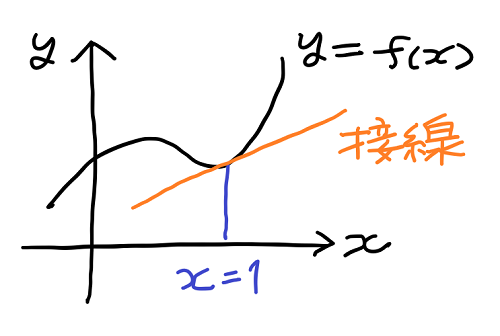
接線は直線なので「 y = a・x + b 」という式で表すことができる。一般的に、この形の式の a の値を傾き、b の値を切片と呼ぶ。
したがって、微分は接線「y = a・x + b 」の a の値を求める方法と言うことができる。
微分は何に使用するのか?
接線の傾き a の値を微分により求めることができるとして、それの何が素晴らしいのかは、実用的な使用例を知らないと理解できない。
機械学習では、予測値と実際の値の差が小さいほど、良い予測だと考える。この誤差(=実際の値 − 予測値)をグラフで表したときに次のような形になったとする。
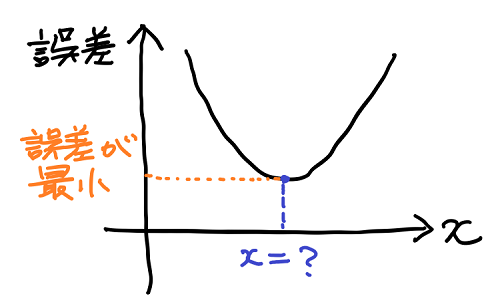
このとき変数 x に依存して変化する誤差が、最小の値を取るような x の値を求めることができれば、最も良い予測を特定することができる。
誤差が最小になる点(x = ?)付近でのグラフに注目すると、次のような性質に気づく。
- x が小さい方から x = ? に近づくにつれて、グラフの傾き(右下がり)が緩くなる。
- x = ? でグラフの傾きが水平になる(傾きがゼロになる)。
- x = ? から x が大きい方に離れるにつれて、グラフの傾き(右上がり)が急になる。
このようにグラフの傾きに着目すると、誤差が最小になる点(x = ?)では傾きがゼロになるという重要な性質を持つことが分かる。
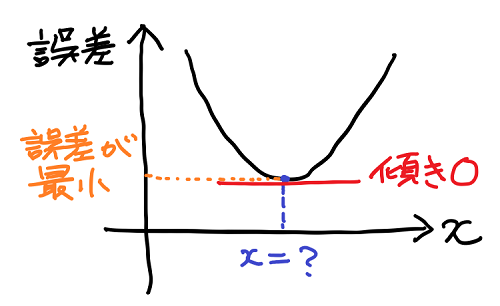
そして傾きと言えば「微分」という数学的手法があるのだった。
微分というツール(数学的手法)を用いれば、ある関数(例えば上のような誤差)が最小になる点(もしくは最大になる点)を導き出すための具体的な方法を与えてくれる、というところに微分のありがたさが存在する。
微分の導関数の定義
グラフの傾きを求める具体的な手法(微分)について考える。
y = f(x) という関数のグラフにおいて、ある点 x における傾きは、その点から少しだけ離れた点 x + h を考えることで求めることができる。
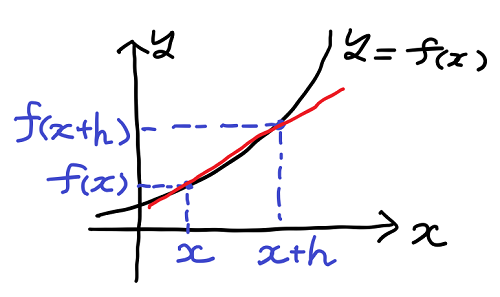
上の図の点 x と点 x + h を通る赤い直線に注目しよう。この直線は点 x における接線とは異なるが、h の値をどんどん小さくしていきゼロに近づければ、その結果は最終的に点 x における接線になるのではないか、と考えられる。
これが微分と呼ばれる接線の傾きを求める手法の考え方だ。この手順を数式で表現してみよう。
赤い直線は y = a・x + b で表すことができる。そして上の図から分かるように、 x に対する y の値は y = f(x) であり、x + h に対する y の値は y = f(x + h) であることから、これを直線の式 y = a・x + b に代入して、次の2つの式が導出される。
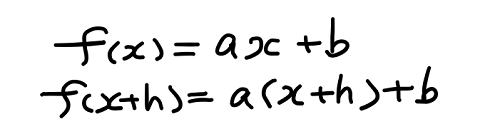
この2つの式の両辺をそれぞれ引いてあげれば、次の式が得られる。
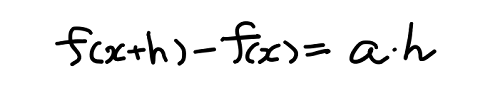
この式の a は赤い直線の傾きであり、これを求めたいわけだから、次のように式を変形する。
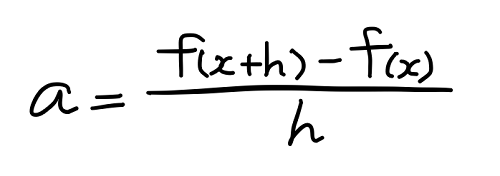
再度確認するが、この式はグラフ y = f(x) 上の点 x と点 x + h を通る赤い直線の傾き a を与えるものだった。そしてこの h の値をゼロに近づければ、a の値は点 x における接線の傾きに近づいていく、というのが微分の考え方だった。
点 x における傾き a を f ‘ (x) で表現し、h の値をゼロに近づける手続きを lim 記号で表現する。このとき、上の式は次のように表現される。
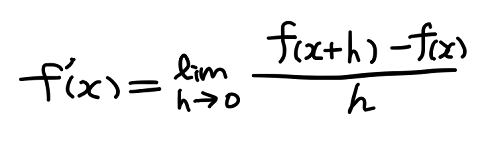
グラフ y = f(x) の点 x における傾き f ‘ (x) を与えるこの式の値は、x を変数とする関数と見なせることから、f(x) の導関数と呼ばれる。
x の 2 乗のグラフを微分してみる
試しに放物線のグラフを微分してみよう。
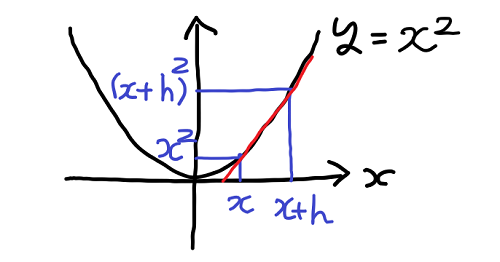
この図のように点 x の傾きを知るには点 x + h について考えればよいのだった。そして上の議論に従い次のような計算を行う。
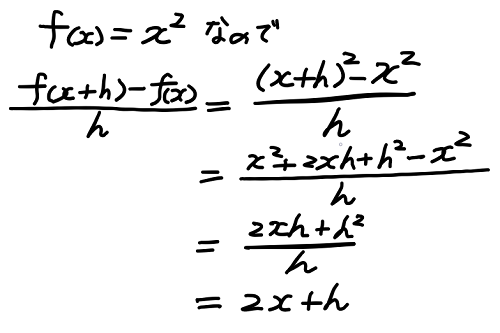
これにより、x の2乗のグラフの点 x と点 x + h を通る赤い直線の傾きは、2・x + h で表せることが分かる。そしてこの h をゼロに近づけることを考えればよいのだった。この 2・x + h を変数 h のグラフとして描いてみると下の図の様な直線になる。
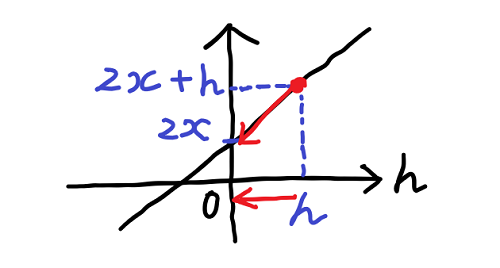
h をゼロに近づければ、2・x + h の値は 2・x に近づき、最終的に 2・x になることが分かる。
つまり、x の2乗のグラフの点 x における傾きは 2・x ということが算出された。
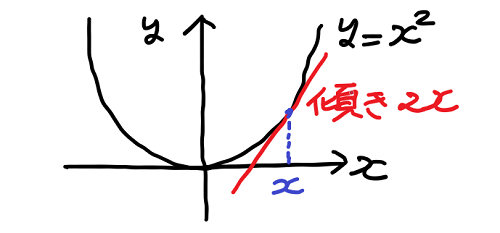
一方で、これは x の2乗という関数から、微分という手続きを経て 2・x というグラフの傾きを与える関数(導関数)を導くことができたことを意味する。つまり x の2乗の導関数について次のように表現することができる。

微分についての公式
上と同様の議論を行うことで、微分(導関数)についてのいくつかの公式を導くことができる。
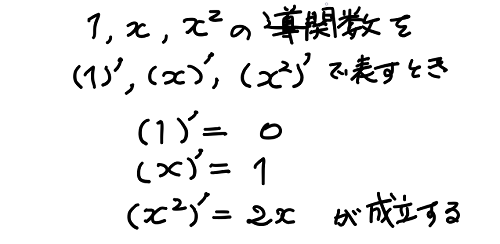
また、関数の和や定数倍についても次のような定理を導くことができる。
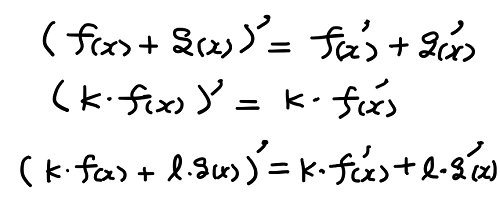
これらの関係を利用すれば、x の2次関数の導関数は簡単に算出できる。
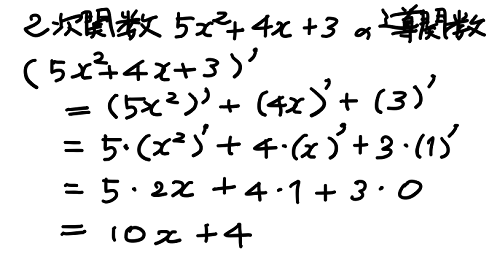
単回帰分析
単回帰分析とは
1つの指標・要因だけに着目し、結果を予測しようという試みを単回帰分析という。複数の指標で結果を予測する場合は、重回帰分析という。
例えば、賃貸物件の家賃を考えたとき、「部屋の広さ」「駅からの距離」など、家賃に影響を与える思われる様々な要因が存在する。
このとき、「部屋の広さ」という1つの指標・要因だけを使って家賃を予測することは、単回帰分析にあたる。
また、この例の「部屋の広さ」のような指標・要因のことを入力変数、「家賃」のような予測値のことを出力変数と呼んだりする。
機械学習の手順
機械学習の手順は3つのステップに分けることができる。
- 「モデル」を決める。
- 「評価関数」を決める。
「モデル」を決める
過去のデータからコンピュータに学習をさせるにあたって、入力変数「部屋の広さ x」と出力変数「家賃 y」の間の関係性を、「y = a・x + b」などの形に仮定してしまうことを指す。また、このような関係性を与える式のことをモデルと呼んでいる。
このモデルは、コンピュータが自ら学習を通して見つけ出すものではない。関係性をモデルで表現できるという仮定に基づいて人間が設定するもの。
「部屋の広さ y」と「家賃 x」の関係性として直線のモデル「y = a・x + b」を仮定した場合、傾き a と切片 b を求めることが、機械学習のゴールとなる。(a, b のことをパラメータと呼ぶ)
「評価関数」を決める
ニューラルネットワークやディープラーニングでは「損失関数」と呼んだりもする。
「部屋の広さ x」と「家賃 y」のデータからモデル「y = a・x + b」のパラメータ a, b を決めるにあたって、良いモデルとは何かという指標が必要になる。
異なるパラメータの組み合わせの中から最善のパラメータの組み合わせを求めるには、パラメータの良し悪しを評価する基準が必要だ。その評価を与えるものを評価関数と呼ぶ。
データの中心化(centering)
機械学習でよく用いられる手法であり、モデルを簡単にすることができる。



